Seeing quantum

When you first learn about quantum mechanics there are two simple examples that can be solved exactly and help give some quantum intuition. Particle in a box and the harmonic oscillator. Recently two experiments have used a scanning tunneling microscope to somewhat let us see these text book examples happening in real systems.

I will do a post on how a scanning tunneling microscope uses tunneling of electrons to image electrons. For now you can think of a STM as a sharp tip that when bought near to the surface can allow electrons to jump onto the tip and let a very small electric current to flow. The voltage of the tip can be used to excite different energy electrons onto the tip. By scanning the tip over the same you can measure the electron density (not position but density more like a localized wave then a particle in this case).

(Image Reference)

The really cool thing is that you get to image the electron density directly which is quantum mechanics is as close as we get to working out where the electron is.

Particle-in-a-box
The particle in a box is the solution to a quantum particle contained with an energy well. In other words the electron cannot get out of some region of space. The potential energy function is usually drawn as:

(Image reference)

The solutions for a quantum particle are

$\psi = \sqrt{\dfrac{2}{L}}sin{\dfrac{n\pi}{L}}x $

Check out how to find the solution at this link

I always found it difficult to think of a physical analogy to this. One system that is often used is a hydrocarbon chain with a conjugated backbone. Electrons are confined along the whole length of the chain and it can be thought of as a analogy to the particle in a box.

A while back I saw a great experiment that seeks to replicate this particle in a box. Using a STM they picked up Palladium atoms and lined up 20 of them. As the electrons were spread out over the whole length and was constrained within the length of the atoms it can be thought of as a analogy to the particle in a box.

STM image of the Palladium atoms lined up 

Using different voltages of the STM tip they were able to excite different energy modes which were found to approximate the solutions for the particle in a box.

(Image from Princples of Modern Chemistry, Oxtoby et al.)

Nilius, N., Wallis, T. M., & Ho, W. (2005). Realization of a particle-in-a-box: electron in an atomic Pd chain. The journal of physical chemistry. B, 109(44), 20657–60. doi:10.1021/jp053496l

Harmonic oscillator

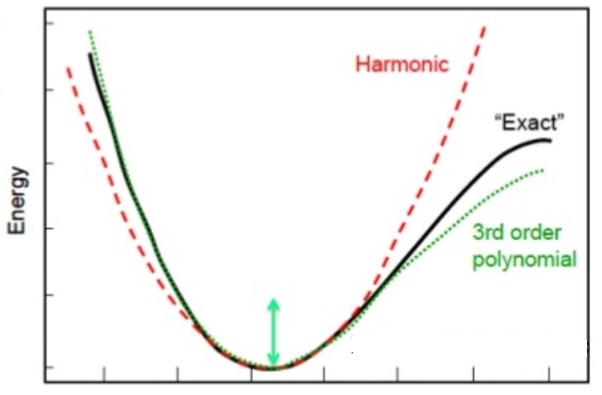
The second system that can be easily solved is a quantum particle in a harmonic (parabolic) potential. The potential for this looks something like this and look a bit like the potential energy of a bond between two atoms.

The harmonic potential (dotted line) approximates the potential energy between two bonding atoms which is shown (solid line) (Image reference)

Think of this as the atoms are vibrating but because everything is quantum you can't vibrate at any frequency you can only vibrate at discrete values. The wave functions can be calculated

By squaring the wave function (left) we get the density or probability (right) of the position of the atoms in this case.

Recently I saw another awesome experiment using the STM and electrons stuck in bits of semiconductor.

By changing the bias voltage on this small quantum dot they were able to excite different vibrational modes of the electron stuck inside of this harmonic potential.

The solid lines are the probability densities and the circles are the current/V as they scan across the dot showing the electrons density.

By scanning the bias voltage they made this nice plot that shows the different vibrational modes being excited as they come to the voltage that matches the energy of the mode.

Teichmann, K., Wenderoth, M., Prüser, H., Pierz, K., Schumacher, H. W., & Ulbrich, R. G. (2013). Harmonic Oscillator Wave Functions of a Self-Assembled InAs Quantum Dot Measured by Scanning Tunneling Microscopy. Nano letters. doi:10.1021/nl401217q