What is this, a batman symbol for ants?

We machined the batman symbol in a single laser shot, five hair widths across!

Here are some 3D plots of the Batman symbol. But seriously, how did we machine a Batman symbol using a laser in one shot, and what do we want to use this for?

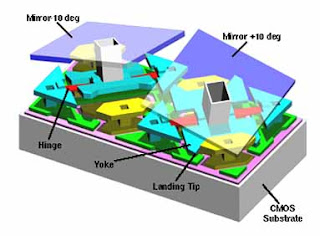
Using tiny mirrors to machine any shape

Digital Micromirror Devices (DMD) are small chips made up of tiny mirrors that can be tilted using the computer. These are really cool devices - looking at a single mirror, you can see the tiny machinery used to move the mirror.

Applying a voltage to the device pulls on and rocks the mirror.

By reflecting certain pixels and deflecting others, you can get a collection of light and dark spots. Using a lens the Fourier transform can be taken of the pixels and a pattern can be generated (Check out my other blog post on Fourier transforms using lenses). This set of spots diffract at the focus of the lens and form the pattern which is the Fourier transform of the amplitude (intensity). This has been used to machine patterns into materials using a single laser shot before.

10.1088/0960-1317/23/3/035005

One of the problems with machining with these DMDs is that to make the spot pattern you have to deflect much of the light away from the lens and you cannot get good efficiencies.

Slowing light down to make patterns

The method we use in the lab is to change the phase of the light reflected off the mirror by having tunable crystals that we can change the refractive index (speed of light through them) of the pixel. Remember the phase shift is a translation of the wave by an angle theta.

https://cms-assets.tutsplus.com/uploads/users/120/posts/19988/image/1000px-Phase_shift.svg.png

The device we use is a liquid crystal on silicon (LCOS) spatial light modulator (SLM). Starting from the bottom, small electrodes can be turned on and off creating an electric field between the top plate and the bottom. A liquid crystal rotates from being flat to upright when the electric field is turned on as the molecule aligns with the electric field lines.

10.1364/OE.22.016087

http://www.sharpsma.com/lcds/lcd-reference-information/twisted-nematic-displays

How does the phase shift create a pattern? Remember from the double slit experiment that a phase shift between waves can lead to constructive and destructive interference far from the sample. This creates a varying intensity profile far from the two slits.

http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/mulslid.html

http://www.olympus-ims.com/vi/ndt-tutorials/intro/breif-history/

Instead of using spherical waves as in the case of the double slit to form constructive and destructive interference, we can shift the phase in such a way that it will interfere to form the pattern we want. One helpful illustration is this experiment in Nature journal that used different thicknesses of a material to cause a phase shift to make a lens made for x-rays.

http://www.nature.com/nature/journal/v401/n6756/fig_tab/401895a0_F2.html

You can see how the different phase shifts introduced from the different thicknesses lead to constructive interference at the focal plane. This is a kind of Fresnel lens. A Fresnel lens cuts up a normal lens into a much lighter collection of curves. These were originally used in lighthouses to collimate the light and send it out to sea.

http://www.teara.govt.nz/en/diagram/6675/fresnel-lens

https://upload.wikimedia.org/wikipedia/commons/thumb/e/e8/Fresnel_lens.svg/2000px-Fresnel_lens.svg.png

As the light comes through the lenses the phase shift is different across the lens and this leads to the focusing or collimating of the light as the different phases interfere.

nphoton.2010.143-f1

The LCOS SLM can give you completely controllable phase shifts. It does this by changing the electric field continuously this allows you to rotate the crystals by a given amount. When the molecules are flat they are along the same direction of the electric field of light and light gets slowed down by the maximum amount when the molecules are upright the light does not interact with the molecules as much as they are perpendicular to the electric field of light. By changing the amount of rotation you can shift the phase by a whole wavelength.

If we wanted to do the same Fresnel lens using an SLM you would provide a grayscale picture where the gray value is the amount of rotation of the molecule and therefore the amount of phase shift.

http://opticalengineering.spiedigitallibrary.org/mobile/article.aspx?articleid=1748345

Something quite fun about the SLM is that you don't need a thick piece of curved glass or a complex custom Fresnel lens - you just shift the phase and the SLM will become a lens using interference.

To make an arbitrary shape like the batman symbol we just have to put in the Fourier transform of the symbol we want and use the complex part of this transform which corresponds to the phase.

Doing the Fourier transform and repeating that pattern a few times gives you this phase mask shown below. Often making this phase mask is presented magically appearing. If you simply do the fourier transform of this using an algorithm called the fast Fourier transform FFT you do not get anything good. This is because you do not have the phase information only the intensity to begin with. We use the Gerchberg-Saxton algorithm to iteratively  improve the phase image so that we can get a nice phase mask that reproduces the intensity profile we need (see the wikipedia page and this python code).

We then add the Fresnel lens to this quite simply we just add each pixel together as the phase goes around in a circle this is not a problem.

Below is the final image if you look carefully you can almost see the batman symbol. This is because a lens takes the Fourier transform of the phase only at the focus but you can see it is starting to change the phase into an intensity profile.

What are we using this for?

I have talked a bit about the ultrafast laser pulses we make in the Photon Factory. The light pulses are around 200 femtoseconds which is 0.0000000000002 s long or a millionth of a billionth of a second. They are so brief in time that they are shorter than the time it takes a molecule to vibrate and therefore can be used to remove the electrons in a material (which allow for bonding and hold everything together) without putting energy into vibrations of the nuclei (which is heat). With all the electrons gone the positively charged nuclei repel each other and leave a perfectly clean hole with no heating effects. Here is a picture below comparing femtosecond to nanosecond laser machined features (a nanosecond is 1 million times faster than a femtosecond).

http://www.industrial-lasers.com/articles/2012/06/femtosecond-laser-micromachining-a-back-to-basics-primer.html

Normally we use a lens to focus the light onto the sample and machine a hole. Focusing a laser beam produces a Gaussian or bell shaped intensity profile. 

http://openspim.org/SPIM_Optics_101/Theoretical_basics

http://openspim.org/SPIM_Optics_101/Theoretical_basics

This is great if you want to make parabolic features but not so good if you want to machine really deep holes quickly. This ends up being the major limitation of femtosecond lasers they are very clean but very slow.

The answer to the problem of how to machine very clean deep holes demands a laser beam with a different intensity profile than the Gaussian beam, called a Bessel beam. This function, unlike the Gaussian, is much tighter and has interesting properties such as energy flow towards the centre of the beam which allows self healing of the beam and the ability to machine very deep holes.

The picture below compares the Gaussian (top) to the Bessel beam (bottom) showing the very concentrated intensity in the centre of the Bessel beam.

10.1002/lpor.201100031

These intensity profiles can really cut through materials and make some astonishingly deep and clean holes. Below is a hole in glass that is 400 nanometres across and 43,000 nm deep. 

Normally these beams are made using axicons or cone lenses. However these are very expensive and hard to make.

https://www.st-andrews.ac.uk/physics/news/old_news/selfhealingbessel.htm

Instead we can use the SLM with a phase mask and use the same trick we used for the Fresnel lens. We break down the axicon into small sections that adjust the phase.

Another interesting thing we can do is add phase masks together so we can have an axicon or other pattern and a focusing Fresnel lens add them together on the phase mask and have both operations occur.

http://www.hamamatsu.com/eu/en/technology/innovation/lcos-slm/index.html

We are using these new beams to machine holes in silicon chips for the semiconductor industry and machining of biological tissues for laser assisted surgery.