This is the final blog post in the series on the paper we recently published on the formation of giant fullerenes (see pt1, pt2 and pt3). In these posts I have been going behind the scenes looking at the techniques and results in context and in less technical language. In this post, I will talk about what holds the fullerenes to the soot during the heating and also look at how large we could make these giant fullerenes.
Link to all of the blog posts on the paper
Part 1 - Energetically fullerenes are unstable and want to coalescence
Part 2 - Weighing fullerenes as they grow
Part 3 - Viewing fullerenes coalescing
Part 4 - Simulating how large we can grow giant fullerenes (this page)
Link to all of the blog posts on the paper
Part 1 - Energetically fullerenes are unstable and want to coalescence
Part 2 - Weighing fullerenes as they grow
Part 3 - Viewing fullerenes coalescing
Part 4 - Simulating how large we can grow giant fullerenes (this page)
How do the small cages stick to the soot at high temperatures?
Oxygen is the short answer. The long answer involves another complex looking instrument called an x-ray photoelectron spectrometer, or XPS for short.
 |
| Credit: nottingham |
Briefly this instrument uses x-rays to excite electrons from the very centre of the atom into the vacuum. The speed of these electrons is then measured to allow the strength of the binding between the core electron and the nuclei to be determined. The reason this instrument is so useful is that small changes in the binding energy of the electrons in the very centre of the atom (core electrons) tells you what is bonded to that atom. Here is a link to a video explaining the instrument in more detail if you are interested.
Oxygen is known to stick to fullerenes easily and to react with fullerenes and irreversibly become integrated into fullerenes when heated. This is why fullerene soot has a shelf life. The mass spectrum below left revealed peaks indicating one two or three oxygen becoming integrated into the fullerenes The XPS spectrum of the carbon in the soot (shown right) shows the integrated oxygen the single bonded form and form crosslinks C-O-C while the carbonyl oxygen cannot C=O.
Oxygen is known to stick to fullerenes easily and to react with fullerenes and irreversibly become integrated into fullerenes when heated. This is why fullerene soot has a shelf life. The mass spectrum below left revealed peaks indicating one two or three oxygen becoming integrated into the fullerenes The XPS spectrum of the carbon in the soot (shown right) shows the integrated oxygen the single bonded form and form crosslinks C-O-C while the carbonyl oxygen cannot C=O.
The C-O-C peak indicates oxygen is acting as a bridging species between the fullerenes and the carbon and also between fullerene cages. Oxygen has previously been shown to anchor fullerenes to nanocones. This would allow the fullerenes to be held to the surface and allow them to coalescence.
We also explored the coalescence of fullerenes bridged by oxygen using a molecular dynamic forcefield that allowed bonds to break and form called ReaxFF.
Similar dynamics can be seen between the all carbon fullerenes coalescing and the oxy-fullerenes. The coalescence is known to be enhanced with oxygen. This could be due to the anchoring effect which makes it more likely they will coalesce or due to relieving the strain at the neck between the fullerenes as they coalescence.
How big can we make them?
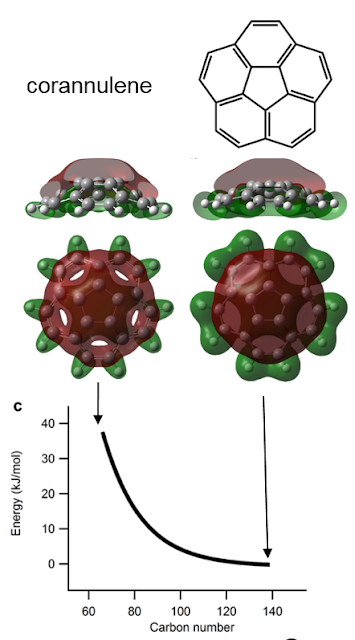
The question of what maximum sized cage can be made is wrapped up with the question of what drives the coalescence. It is known that the top and bottom surface of graphite is not reactive and only when you add in a pentagon and strain the structure does it become reactive. This has also been shown with simulations of fullerenes fusing. We, therefore, considered only the pentagon as being the reactive site. As the fullerenes become smaller the pentagon site becomes more strained. We simulated this by puckering a small bowl molecule that is the simplest curved subunit corannulene. This straining could be related with a certain increase in the energy and we hypothesised that the higher reactivity of the smaller cages is linearly dependent with this energy (Bell-Evans-Polanyi principle).
To see if this scaling is appropriate we chose a simple system the laser ablation and detection of C60 and C70 in a mass spectrometer (the toluene extract from the soot extraction process was used). We used a high laser power to produce dimers and trimers of C60 and C70. In the gas phase you can assume only two molecules are reacting at a time and this lets you write down a set of equation you can solve using the computer. Below the experimental and simulation mass spectra can be compared.
The simulation was able to describe the formation of dimers and trimers. Differences between the experiment and the simulation include the right skew to the mass spectrum in the experiment which is due to C2 being ejected. Another difference is the higher concentration of C60 and C70 dimers indicating that C60 and C70 are indeed less reactive than the other cages. The reasonable agreement with the size of fragments that are formed suggests the coalescence at low temperatures is driven by the strain at the pentagonal carbon atoms. This would allow cages up to ~300 carbon atoms to be formed from low temperature strain driven reactions. Below is an interactive 3D model of $\text{C}_{320}$ click and drag the structure to see the structure of a similar sized giant fullerene.
So what?
The first thing these results allowed us to do is comment on fullerene formation mechanisms. The mass spectrum provides a second experimental validation of the log-normal distribution of fullerene cages found previously in the gas phase. This log-normal distribution indicates a process of size dependent growth and/or coalescence occurring. This rules out some mechanisms where the fullerenes remain in contact and exchange carbon, which is seen in droplets (Ostwald ripening). This would produce a distribution skewed towards the higher masses which is the opposite of what is observed. Also, disproportionation reactions would lead to a normal distribution of masses as shown by Curl et al. which is not seen. The log-normal distribution could be achieved through $\text{C}_2$ ingestion/ejection where the smaller fullerenes are more reactive to free $\text{C}_2$. Or by fullerenes in the gas phase fragmenting and coalescing dynamically. We are currently working on the kinetic model to include these features.
The second comment is on how you would go about making greater quantities of giant fullerenes preferably without oxygen. One option is to modify the arc synthesis of fullerenes, by providing more time and higher temperatures inside the carbon plasma you could tuned the reactor to produce larger structures.
Finally, the internal volume of these larger fullerenes are significantly larger than the magic number fullerene C$_{60}$ and C$_{70}$ and there is potential to trap inside the cages many atoms or even perhaps molecules. It is also an interesting thought to consider how much bigger these fullerenes could be produced. The paper mentioned in the first blog post of shrinking giant fullerenes imaged much larger fullerenes C$_{1000}$ which are thought to come from nanotubes in that study. This suggests further enlarging is possible.
If you got through all of those blog posts well done! Please post any comments if you have any questions about the methods used or the interpretation of the results.
If you got through all of those blog posts well done! Please post any comments if you have any questions about the methods used or the interpretation of the results.




No comments:
Post a Comment