Sunday, 3 December 2017
Describing chemistry at all scales
Sunday, 12 November 2017
Nanotechnology right under our noses
 |
| Image sources: link, link, link |
In the past, gold nanoparticles were used to produce brilliant reds in stained glass windows and nanoscale tubes were woven into Damascus steel to make strong, sharp swords. These technologies were used without full knowledge of the processes involved, or safety concerns; however, the recent breakthrough in nanotechnology is our understanding and control of nanoscale structures.
My colleagues and I at the Department of Chemical Engineering and Biotechnology have found a common nanostructure that unites a variety of carbon materials, many of which are right under your nose. Water and air filters use activated carbon and vehicles produce soot - even your tennis racket and bike that contain carbon fibres.
You might be familiar with the layered structure of graphite: carbon atoms are arranged hexagonally in sheets that can easily glide past each other. This makes graphite a great material for pencil lead or a solid lubricant, but not as a filter or a bike frame. When graphite starts to become curved and interlinked is when the structure takes on its exceptional and diverse properties.
We ran quantum chemical calculations on the university’s supercomputers to understand what occurs when curvature is integrated into graphitic sheets through the replacement of a hexagonal ring of carbon with a pentagonal ring. This leads to a permanent bend in the structure that shuttles electrons from one side of the sheet to the other. This electric polarisation significantly increases the interaction of curvature-containing carbon material with molecules and itself, explaining how a relatively inert graphite can become strong and porous.
The next step for us is to explore how we can use our discoveries to reduce the emission of soot from vehicles, improve water filtration and improve the many carbon nanostructures that are right under our noses.
Thursday, 9 November 2017
Polar aromatic molecules
In short
- We found that this curving of the molecules shifted the electrons from the concave to the convex side of the molecule which makes quite a large electric field.
- This is quite a strange finding mainly because most aromatic molecules are usually considered electrically non-polar.
- These curved molecules have been spotted (using electron microscopes) in soot particles, carbon battery electrodes and carbon water filters.
- The electric field around these molecules will have a huge impact on how they interact with polar molecules such as water and many pollutants the electric field will also provide significant interactions with ions such as lithium used in batteries.
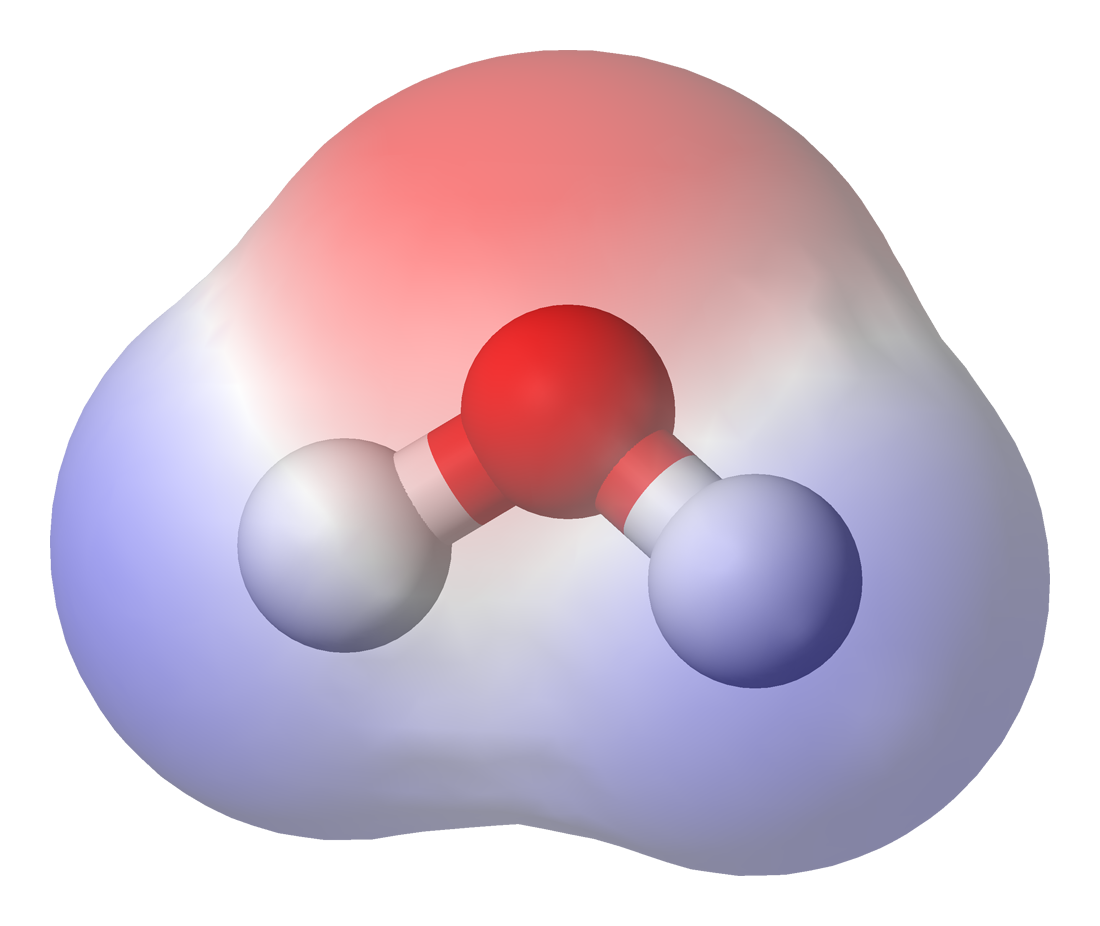
What are polar molecules?
  |
| Credit: link |
| Credit: link and recoloured |
  |
| Credit: CSIC |
 |
| Credit: Qwerter |
If you have a balloon handy you can do a simple experiment to convince yourself that water is polar. Rubbing a balloon with a cloth or on your head removes positive charge and leaves the balloon with a negative charge. Holding the balloon near a stream of water the positive side of the water molecule will be attracted to the negative charge on the balloon and it will bend the water toward itself.
 |
Credit: Link
|
| Table of the dipole moment in Debye units (1 D = 3.336×10^-30 C m) taken from Israelachvili 1992 | ||
|---|---|---|
| Molecule | Formula | Dipole moment |
| Ethane | $\text{C}_2\text{H}_6$ | 0 |
| Benzene | $\text{C}_6\text{H}_6$ | 0 |
| Carbon tetrachloride | $\text{CCl}_4$ | 0 |
| Carbon dioxide | $\text{CO}_2$ | 0 |
| Chloroform | $\text{CCl}_3$ | 1.06 |
| Hydrochloric acid | $\text{HCl}$ | 1.08 |
| Ammonia | $\text{NH}_3$ | 1.47 |
| Phenol | $\text{C}_6\text{H}_5\text{OH}$ | 1.5 |
| Ethanol | $\text{C}_2\text{H}_5\text{OH}$ | 1.7 |
| Water | $\text{H}_2\text{O}$ | 1.85 |
| Cesium Chloride | $\text{CsCl}$ | 10.4 |
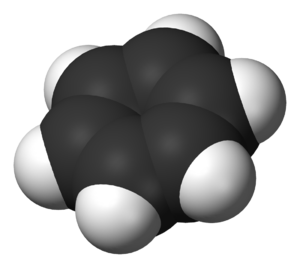
Are planar aromatic molecules polar?
Plotting below the electrostatic potential of these two molecules looking side on (perpendicular to the aromatic plane) the electric field around planar aromatic molecules can be viewed. Around the hydrogen atoms, often called the rim of the PAH, the potential is positive. The top and bottom near the carbon atoms is negative. This can be explained by the bonding but we will leave this for another post.
Curved aromatics are polar
We used a supercomputer to calculate the electron density around some very large curved aromatic molecules. From this we could determine the dipole moment with very good accuracy (less than 2% error for corannulene compared with experiment). The figure below shows the strong scaling of the dipole moment with the size of the molecules. The size range found in soot and other carbon materials is around 10-20 aromatic rings shown as the shaded grey area. This indicates that curved fragments in carbon materials can have a significant dipole moment of 2-6 D.
Why is this result so exciting?
- In batteries positively charged lithium ions will interact strongly with the dipole moment on the curved molecules.
- In soot formation charged chemi-ions will interact strongly with curved aromatic molecules in the flame.
- In activated carbon a strong interaction is expected between the dipole moment and adsorbents that are charged or polar.
Simulating carbon materials with curvature in the computer
Wednesday, 1 November 2017
Curving aromatic molecules
  |
| Credit: link |
 |
| Credit: Paula Soler-Moya |
 |
| Credit: Ikea |
Molecular dynamics in Python
Molecular simulations have been heralded as the new computational microscope that are helping us understand how molecules interact with each other and how they self assemble into complex structures. A molecular dynamics simulation is a particular type of simulation which generally approximates the intermolecular forces/energy using mathematical functions. The impact of temperature is often included (which usually drives molecules apart) and the interplay between this thermal energy and the intermolecular energy gives rise to the self assembly processes.
There are many different applications to molecular dynamics including describing the interactions between drugs and protein binding sites and describing the self-assembly of molecular systems like lipid bilayers and colloids. Colleagues and I have used molecular dynamics to simulate the self assembly of soot and the dynamics of polymers for CO2 separation. I have put this short example together using the simplest potential - the Lennard-Jones potential. This potential describes the attraction at long distances and repulsion at short distances and can model the behaviour of gases such as argon and helium quite well. This example is based on the fortran code written by Furio Ercolessi, SISSA, Trieste. This example is written in the ipython notebook and the python scripts can be copied and run on any computer with python 2 installed along with the numpy and matplotlib libraries.
Molecular dynamics basics¶
Most molecular dynamics programs use classical approximations (Newtonian mechanics) to describe the energy of the system as a function of the positions of the atoms/particles.
$$ E(\textbf{r}) $$We can use Newton's second law to describe the motion of the particles through time.
$$ F = m \textbf{a} = m \frac{d^{2}\textbf{v}}{dt^{2}}$$The force can be calculated in one dimension by taking the derivative with respect to $x$ (or in three dimensional vector notation, the gradient $\nabla$) of the energy.
$$ F = -\frac{dE}{dx} = -\nabla E(\textbf{r}) $$So the first step is to calculate the forces on the particles by describing the intermolecular potential energy.
Lennard-Jones potential¶
The potential energy of the 12-6 Lennard-Jones potential is given as
$$ E_{LJ}(r)=4\epsilon\left[ \left( \frac{\sigma}{r}\right)^{12}- \left( \frac{\sigma}{r}\right)^{6} \right] $$
$ \sigma $ is the radius where the potential is zero and is defined as the van der waals radius. $ \epsilon $ is the energy minimum of the interaction (see the figure below).
We don't want to compute long range interactions as they will be negligible. We therefore apply a cutoff past $r/\sigma=2.5$. However, as the particles move past the cutoff distance there will be a small jump in the energy, which is not realistic, so we shift the potential so that the potential goes to zero at $r/\sigma=2.5$.
Below is a plot of the Lennard-Jones potential with the shifted potential shown for comparison.
#Import a plotting libraries and a maths library
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
r = np.linspace(0.01,3.0,num=500) # Make a radius vector
epsilon = 1 # Energy minimum
sigma = 1 # Distance to zero crossing point
E_LJ = 4*epsilon*((sigma/r)**12-(sigma/r)**6) # Lennard-Jones potential
plt.figure(figsize=[6,6])
plt.plot(r,E_LJ,'r-',linewidth=1,label=r" $LJ\; pot$") # Red line is unshifted LJ
# The cutoff and shifting value
Rcutoff = 2.5
phicutoff = 4.0/(Rcutoff**12)-4.0/(Rcutoff**6) # Shifts the potential so at the cutoff the potential goes to zero
E_LJ_shift = E_LJ - phicutoff # Subtract the value of the potential at r=2.5
plt.plot(r[:415],E_LJ_shift[:415],'b-',linewidth=1,label=r"$LJ\; pot\; shifted$") # Blue line is shifted
#Plot formatting
plt.rc('text', usetex=True)
plt.rc('xtick', labelsize=20)
plt.rc('ytick', labelsize=20)
plt.title(r"$Lennard-Jones\; potential$",fontsize=20)
plt.xlim([0.0,3.0])
plt.ylim([-1.5,1.5])
plt.ylabel(r"$E_{LJ}/\epsilon$",fontsize=20)
plt.xlabel(r"$r/\sigma$",fontsize=20)
plt.legend(frameon=False,fontsize=20)
plt.axhline(0, color='grey',linestyle='--',linewidth=2)
plt.axvline(1, color='grey',linestyle='--',linewidth=2)
<matplotlib.lines.Line2D at 0x10b68fac8>
Reduced units¶
By choosing our units we can remove any constants and get a general behaviour for all gases. Mass, sigma, epsilon and the Boltzmann constant are set to equal one. Reduced coordinates are used for the other variables which are derived from the parameters set to one.
$$ x^{*} = \frac{x}{\sigma} $$$$ v^{*} = v\frac{t^{*}}{\sigma} $$$$ t^{*} = t\left(\frac{\epsilon}{m \sigma^{2}} \right)^{1/2} $$$$ E^{*} = \frac{E}{\epsilon} $$$$ F^{*} = f\frac{\sigma}{\epsilon} $$$$ P^{*} = P \frac{\sigma^{3}}{\epsilon}$$$$ \rho^{*} = \rho \sigma^{dimensions} $$$$ T^{*} = T \frac{k_{b}}{\epsilon} $$Where $k_{b}$ is Boltzmann's constant.
This may seem complicated but it allows all of the equations to be written very simply in the program. This also gives us physical insight - for example, the reduced temperature is the ratio of the thermal energy $k_{B} T$ to the energy of the intermolecular interactions $\epsilon$.
Periodic boundary conditions¶
Periodic boundary conditions allow for an approximation of an infinitely sized system by simulating a simple unit cell. This is illustrated below. The black box is the only cell we simulate; the tiled images around it are there for illustration. The green particle moves past the top boundary of the unit cell and are moved to the bottom of the box with the same velocity (illustrated by the red dashed line). This boundary condition keeps the volume and number of particles constant in the simulation.
By I, Grimlock, CC BY-SA 3.0, Link
Calculating the forces¶
As mentioned above, the forces between particles can be calculated from the derivative/gradient of their potential energy. $\textbf{F}=-\frac{1}{r}\nabla E(\textbf{r})$ (in spherical coordinates)
$$ \textbf{F} = -\frac{1}{r}\nabla E_{LJ}(\textbf{r}) = -\frac{1}{r}\frac{d E_{LJ}}{d \textbf{r}} = -24\left[2\left(\frac{\sigma}{\textbf{r}}\right)^{14} - \left(\frac{\sigma}{\textbf{r}}\right)^{8}\right] $$Periodic boundary conditions have to be considered when we compute the forces between particles because a particle near the boundary of the unit cell has to be able to feel the force from a particle on the other side of the unit cell. For example, the pink particle above will feel the force from the green particle, even though they are far from each other because they are near opposite boundaries.
In order to easily implement periodic boundary conditions, scaled box units are used so that the particle positions are always between -0.5 and 0.5. If the distance between the particles is greater than half the scaled box units, the interaction with the particle in the next box are considered.
def Compute_Forces(pos,acc,ene_pot,epsilon,BoxSize,DIM,N):
# Compute forces on positions using the Lennard-Jones potential
# Uses double nested loop which is slow O(N^2) time unsuitable for large systems
Sij = np.zeros(DIM) # Box scaled units
Rij = np.zeros(DIM) # Real space units
#Set all variables to zero
ene_pot = ene_pot*0.0
acc = acc*0.0
virial=0.0
# Loop over all pairs of particles
for i in range(N-1):
for j in range(i+1,N): #i+1 to N ensures we do not double count
Sij = pos[i,:]-pos[j,:] # Distance in box scaled units
for l in range(DIM): # Periodic interactions
if (np.abs(Sij[l])>0.5):
Sij[l] = Sij[l] - np.copysign(1.0,Sij[l]) # If distance is greater than 0.5 (scaled units) then subtract 0.5 to find periodic interaction distance.
Rij = BoxSize*Sij # Scale the box to the real units in this case reduced LJ units
Rsqij = np.dot(Rij,Rij) # Calculate the square of the distance
if(Rsqij < Rcutoff**2):
# Calculate LJ potential inside cutoff
# We calculate parts of the LJ potential at a time to improve the efficieny of the computation (most important for compiled code)
rm2 = 1.0/Rsqij # 1/r^2
rm6 = rm2**3.0 # 1/r^6
rm12 = rm6**2.0 # 1/r^12
phi = epsilon*(4.0*(rm12-rm6)-phicutoff) # 4[1/r^12 - 1/r^6] - phi(Rc) - we are using the shifted LJ potential
# The following is dphi = -(1/r)(dV/dr)
dphi = epsilon*24.0*rm2*(2.0*rm12-rm6) # 24[2/r^14 - 1/r^8]
ene_pot[i] = ene_pot[i]+0.5*phi # Accumulate energy
ene_pot[j] = ene_pot[j]+0.5*phi # Accumulate energy
virial = virial + dphi*np.sqrt(Rsqij) # Virial is needed to calculate the pressure
acc[i,:] = acc[i,:]+dphi*Sij # Accumulate forces
acc[j,:] = acc[j,:]-dphi*Sij # (Fji=-Fij)
return acc, np.sum(ene_pot)/N, -virial/DIM # return the acceleration vector, potential energy and virial coefficient
Temperature¶
Temperature is a macroscopic quantity. Microscopically it is less well defineddue to the low number of particles. However, if we use the kinetic energy of the parameters we can calculate the temperature.
$$ E_{K}=\frac{1}{2} mv^{2} $$$$ k_{B} T = \frac{2}{3}\sum_{N}E_{K} $$Where we sum over all $N $ atoms. We will use this in order to scale the velocities to maintain a constant temperature (remember we are using reduced units so $k_{B}=1$ and $m=1$).
The function below calculates the temperature given the velocity of the atoms/particles.
def Calculate_Temperature(vel,BoxSize,DIM,N):
ene_kin = 0.0
for i in range(N):
real_vel = BoxSize*vel[i,:]
ene_kin = ene_kin + 0.5*np.dot(real_vel,real_vel)
ene_kin_aver = 1.0*ene_kin/N
temperature = 2.0*ene_kin_aver/DIM
return ene_kin_aver,temperature
Molecular dynamics program¶
The molecular dynamics program contains the instructions for the computer to use to move the particles/atoms through time. Most often this is written in Fortran and C; these compiled languages are orders of magnitude faster than Python, however a scripting language like Python is helpful to provide understanding about how molecular dynamics is implemented.
The main steps in a molecular dynamics simulation are:
- Initialise the position of particles
- Calculate the pairwise forces on the particles by calculating the gradient of the potential energy $ F = \nabla E(\textbf{r})=1/r\partial E(\textbf{r})/\partial r$
- Compute the new positions by integrating the equation of motion (we will use the velocity Verlet algorithm)
- Apply a thermostat to maintain the temperature at the set value (we will use the velocity scaling for temperature control)
- Go back to step 2, recompute the forces and continue until the maximum number of steps
Initialising the particles¶
DIM = 2 # Dimensions
N = 32
BoxSize = 10.0#6.35
volume = BoxSize**DIM
density = N / volume
print("volume = ", volume, " density = ", density)
pos = np.zeros([N,DIM])
pos = np.genfromtxt('output.dat',skip_header=1) # Load positions from file
pos = pos[:,:DIM]/BoxSize
MassCentre = np.sum(pos,axis=0)/N
for i in range(DIM):
pos[:,i] = pos[:,i]-MassCentre[i]
volume = 100.0 density = 0.32
Integrating the equations of motion¶
We will make use of the velocity Verlet integrator which integrates Newton's equations of motion in 1D:
$$ \frac{dx}{dt}=v\; and \; \frac{dv}{dt}=\frac{dF(x)}{m} $$The velocity Verlet algorithm spilts the velocity update into two steps intially doing a half step then modifing the acceleration and then doing the second velocity update. Written in full, this gives:
- Calculate $x(t+\Delta t) = x(t)+v\left(t+\frac{1}{2}\right)\Delta t$
- Calculate $v\left(t+\frac{1}{2}\Delta t\right)= v(t)+\frac{1}{2}a(t)\Delta t $
- Derive $a(t+\Delta t)$ from the interaction potential using $x(t+\Delta t)$
- Calculate $v(t+\Delta t)=v\left(t+\frac{1}{2}\right)+\frac{1}{2}a(t+\Delta t) \Delta t$
Between step 1 and 2 we rescale the velocities to maintain the temperature at the requested value.
The output is saved in the same folder as the ipython notebook as traj.xyz and can be opened by Avogadro or VMD.
# Setting up the simulation
NSteps=10000 # Number of steps
deltat = 0.0032 # Time step in reduced time units
TRequested = 0.5# #Reduced temperature
DumpFreq = 100 # Save the position to file every DumpFreq steps
epsilon = 1.0 # LJ parameter for the energy between particles
# Main MD loop
def main(pos,NSteps,deltat,TRequested,DumpFreq,epsilon,BoxSize,DIM):
# Vectors to store parameter values at each step
N = np.size(pos[:,1])
ene_kin_aver = np.ones(NSteps)
ene_pot_aver = np.ones(NSteps)
temperature = np.ones(NSteps)
virial = np.ones(NSteps)
pressure = np.ones(NSteps)
ene_pot = np.ones(N)
vel = (np.random.randn(N,DIM)-0.5)
acc = (np.random.randn(N,DIM)-0.5)
# Open file which we will save the outputs to
f = open('traj.xyz', 'w')
for k in range(NSteps):
# Refold positions according to periodic boundary conditions
for i in range(DIM):
period = np.where(pos[:,i] > 0.5)
pos[period,i]=pos[period,i]-1.0
period = np.where(pos[:,i] < -0.5)
pos[period,i]=pos[period,i]+1.0
# r(t+dt) modify positions according to velocity and acceleration
pos = pos + deltat*vel + 0.5*(deltat**2.0)*acc # Step 1
# Calculate temperature
ene_kin_aver[k],temperature[k] = Calculate_Temperature(vel,BoxSize,DIM,N)
# Rescale velocities and take half step
chi = np.sqrt(TRequested/temperature[k])
vel = chi*vel + 0.5*deltat*acc # v(t+dt/2) Step 2
# Compute forces a(t+dt),ene_pot,virial
acc, ene_pot_aver[k], virial[k] = Compute_Forces(pos,acc,ene_pot,epsilon,BoxSize,DIM,N) # Step 3
# Complete the velocity step
vel = vel + 0.5*deltat*acc # v(t+dt/2) Step 4
# Calculate temperature
ene_kin_aver[k],temperature[k] = Calculate_Temperature(vel,BoxSize,DIM,N)
# Calculate pressure
pressure[k]= density*temperature[k] + virial[k]/volume
# Print output to file every DumpFreq number of steps
if(k%DumpFreq==0): # The % symbol is the modulus so if the Step is a whole multiple of DumpFreq then print the values
f.write("%s\n" %(N)) # Write the number of particles to file
# Write all of the quantities at this step to the file
f.write("Energy %s, Temperature %.5f\n" %(ene_kin_aver[k]+ene_pot_aver[k],temperature[k]))
for n in range(N): # Write the positions to file
f.write("X"+" ")
for l in range(DIM):
f.write(str(pos[n][l]*BoxSize)+" ")
f.write("\n")
if(DIM==2):
import matplotlib.pyplot as plt
from IPython import display
plt.cla()
plt.xlim(-0.5*BoxSize,0.5*BoxSize)
plt.ylim(-0.5*BoxSize,0.5*BoxSize)
for i in range(N):
plt.plot(pos[i,0]*BoxSize,pos[i,1]*BoxSize,'o',markersize=20,)
display.clear_output(wait=True)
display.display(plt.gcf())
#print(ene_kin_aver[k], ene_pot_aver[k], temperature[k], pressure[k])
f.close() # Close the file
return ene_kin_aver, ene_pot_aver, temperature, pressure, pos
ene_kin_aver, ene_pot_aver, temperature, pressure, pos = main(pos,NSteps,deltat,TRequested,DumpFreq,epsilon,BoxSize,DIM)
Done
# Plot all of the quantities
def plot():
plt.figure(figsize=[7,12])
plt.rc('xtick', labelsize=15)
plt.rc('ytick', labelsize=15)
plt.subplot(4, 1, 1)
plt.plot(ene_kin_aver,'k-')
plt.ylabel(r"$E_{K}$", fontsize=20)
plt.subplot(4, 1, 2)
plt.plot(ene_pot_aver,'k-')
plt.ylabel(r"$E_{P}$", fontsize=20)
plt.subplot(4, 1, 3)
plt.plot(temperature,'k-')
plt.ylabel(r"$T$", fontsize=20)
plt.subplot(4, 1, 4)
plt.plot(pressure,'k-')
plt.ylabel(r"$P$", fontsize=20)
plt.show()
plot()
print("Temperature = ", np.average(temperature), "+-", 2*np.std(temperature))
Temperature = 0.499976604421 +- 0.00580962776371
print("Pressure = ", np.average(pressure), "+-", 2*np.std(pressure))
Pressure = 0.273148208667 +- 0.365424653066
The thermostat appears to be holding the temperature close to the requested value of $T^{*}=0.5$.
# Stylings from http://lorenabarba.com
from IPython.core.display import HTML
def css_styling():
styles = open("custom.css", "r").read()
return HTML(styles)
css_styling()
Implementation in LAMMPS¶
Lammps is a very fast molecular dynamics package. The input file is below and performs a much longer simulation in less than a minute. At the top of the this article is the animated video from the simulation where the temperature was reduced from $T^*=$1.0 to $T^*=$0.2 showning the nucleation of a crystal.
# 2d Lennard-Jones melt
variable x index 1
variable y index 1
variable z index 1
variable xx equal 40*$x
variable yy equal 20*$y
variable zz equal 20*$z
units lj
atom_style atomic
dimension 2
lattice hex 0.8442 #Set the lattice vector
region box block 0 ${xx} 0 ${yy} 0 1 # Make region for the periodic box
region two block 5 15 5 15 0 1 # Make a region for where the atoms will begin
create_box 1 box
create_atoms 1 region two # Create the atoms
mass 1 1.0
velocity all create 1.44 87285 loop geom # Set their initial velocity which will be scaled during the simulation
pair_style lj/cut 2.5 # Define the intermolecular interaction with the Lennard-Jones function with a cutoff of 2.5
pair_coeff 1 1 1.0 1.0 2.5 # Setting the sigma and epsilon values
# This neighbor list improves the efficiency of the calculation by only calculating interactions with particles within cutoff+0.3
neighbor 0.3 bin
neigh_modify delay 0 every 20 check no
dump 1 all xyz 200 dump.lj #Saves the trajectory to a file to open in VMD
fix 1 all nve # Performs an integration to move the sample through time
fix 2 all enforce2d # Make sure there is no forces in the z direction
fix 3 all temp/rescale 1 1.0 0.2 0.02 0.5 # This rescales the velocity to keep the temperature constant.
run 1000000 #run for this number of steps the default timestep for lj is 0.005 tau